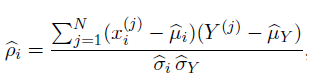اگر Y = M(X) مدل ریاضیاتی پدیده مورد نظر تابعی از متغیرهای تصادفی (Random Variable) بصورت (X1,X2,...,XM) باشد، آنالیز حساسیت (Sensitivity Analysis) مشخص می کند که مدل مورد نظر بر اثر تغییر هر یک از متغیرهایش چگونه دستخوش تغییر می شود.
یکی از مهم ترین کاربردهای آنالیز حساسیت، کاهش پیچیدگی مدل های ریاضی با حذف پارامترهای کمتر تاثیرگذار می باشد.
در مجموعه مقالات پیش رو به معرفی تعدادی از روش های آنالیز حساسیت که دارای رویکرد احتمالاتی می باشند، خواهیم پرداخت.
یکی از ساده ترین و در عین حال جزو کاراترین روش های آنالیز حساسیت، بررسی ضریب همبستگی بین پاسخ مدل (Y) و هریک از متغیرهای تصادفی (Xi) می باشد. این روش تحت عنوان Input/Output Correlation شناخته می شود.
برای این روش لازم است تا N دسته متغیر تصادفی X با روش های شبیه سازی مانند مونت-کارلو (Monte Carlo) تولید شود. براساس هریک از این بردارهای متغیر تصادفی تولید شده، پاسخ مدل محاسبه می شود. بعبارتی خواهیم داشت:
در نهایت، با محاسبه میانگین و انحراف معیار پارامترهای ورودی و پاسخ برای هریک از N حالت فوق، ضریب همبستگی متغیر تصادفی Xi به پاسخ مدل بصورت زیر محاسبه می گردد:
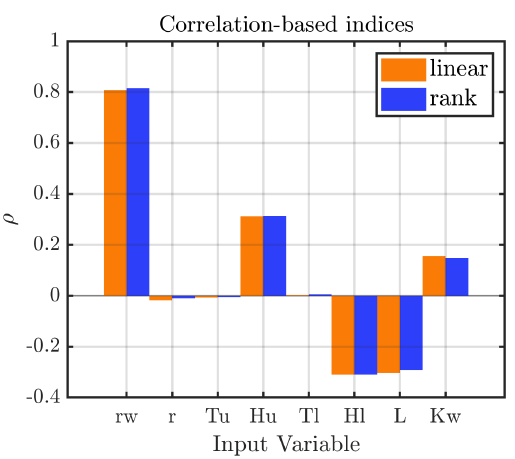
نمونه ای از این محاسبات در شکل فوق نشان داده شده است. بدیهی است متغیرهایی که دارای ضریب همبستگی بالاتری باشند، از تاثیرگذاری بیشتری برخوردارند. گرچه باید توجه شود که این روش برای مسائلی با هبمستگی غیرخطی شدید مابین متغیرهای ورودی چندان کارا نخواهد بود.